Moving Average (MA)
Allgemein
Der Moving Average (MA) ist einer der am häufigsten benutzten Indikatoren und zeigt den Durchschnittspreis eines Assets über eine zuvor festgelegte Periode an. Im Deutschen wird der Moving Average auch "Gleitender Durchschnitt” genannt. Der Moving Average wird berechnet, um kurzfristige Preisschwankungen zu glätten, indem fortlaufend der Durchschnittspreis eines Assets berechnet wird. So hilft der Moving Average dabei über kurzfristige Kursschwankungen hinwegzusehen und Trends zu erkennen. Der Moving Average wird somit am häufigsten als Trendfolgeindikator eingesetzt. Die Berechnungsperiode kann flexibel eingestellt werden, bei kleineren Perioden ist die Sensitivität gegenüber kurzfristigen Schwankungen jedoch höher. Häufig werden als Periodendauer die Werte 15, 20, 30, 50, 100, 150 und 200 Tage gewählt. Es gibt drei wichtige Moving Average Typen: Simple, Exponential und Weighted.
Typen von Moving Averages
Simple Moving Average (SMA)
Beim Simple Moving Average wird der Durchschnittspreis der ausgewählten Perioden berechnet. Es wird also der Durchschnitt der Schlusskurse aus den letzten n-Tagen gebildet. Die Berechnungsgrundlage für die Berechnung des Durchschnittes bewegt sich also mit jedem neuen Tag nach vorn. Daher wird der Moving Average auch im Deutschen "Gleitender Durchschnitt" genannt. Es ergibt sich eine Linie, da der Wert für jeden Tag fortlaufend berechnet wird. Der SMA wird mit der folgenden Formel berechnet:
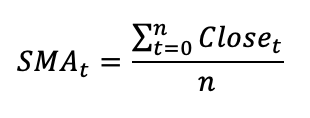
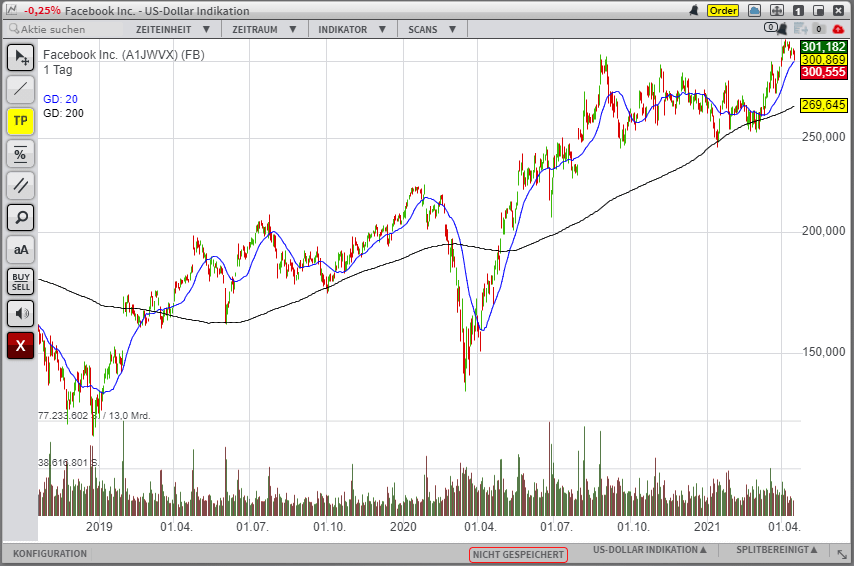
Die 20-Tage-Linie (blau) reagiert deutlich sensibler auf kurzfristige Kursschwankungen als die 200-Tage-Linie (schwarz).
Exponential Moving Average (EMA)
Der Exponential Moving Average wurde als Verbesserung des Simple Moving Average entwickelt. Beim Exponential Moving Average werden Preise aus neueren Perioden höher gewichtet als Preise aus älteren Perioden. Jüngere Preisänderungen haben also einen größeren Einfluss als beim Simple Moving Average. Das hat zur Folge, dass der EMA wesentlich glatter verläuft als der SMA und auch näher am tatsächlichen Preisverlauf liegt.
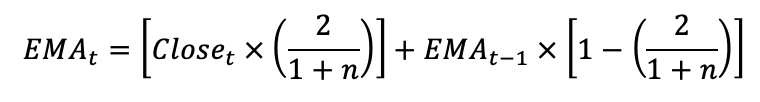
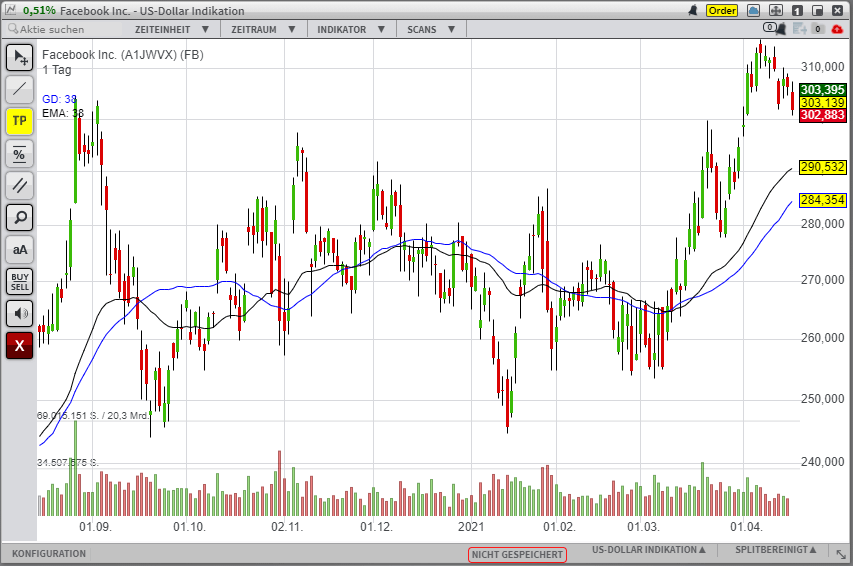
Der Exponential Moving Average (schwarz) verläuft etwas glatter und liegt näher am Preisverlauf als der Simple Moving Average (blau).
Double Exponential Moving Average (DEMA)
Der Double Exponential Moving Average ist eine Weiterentwicklung des Exponential Moving Average und hat den Zweck, den Linienverlauf noch stärker zu glätten um falsche Signale zu eliminieren. Er wurde von Peter Mulloy entwickelt und 1994 veröffentlicht. Für die Berechnung wird zunächst der EMA der Periode n berechnet. Anschließend wird von diesem EMA ein weiterer EMA gebildet, wodurch man einen geglätteten EMA erhält. Der ursprüngliche EMA der Periode n wird anschließend mit 2 multipliziert und es wird der der geglättete EMA subtrahiert.
![]()
Triple Exponential Moving Average (TEMA)
Vom Aufbau ähnelt der Triple Exponential Moving Average dem DEMA, was daran liegt, dass der Triple Exponential Moving Average ebenfalls von Peter Mulloy entwickelt wurde. Der Zweck dieser Abwandlung des EMA ist es, den Linienverlauf stärker zu glätten. Zur Berechnung muss als erstes der EMA berechnet werden, in der Formel als EMA1 bezeichnet. Dann wird ein weiterer EMA (EMA2) vom ursprünglichen EMA1 gebildet. Vom EMA2 wird dann erneut ein EMA (EMA3) gebildet. In die Formel eingesetzt erhält man den Triple Exponential Moving Average.
![]()
![]()
![]()
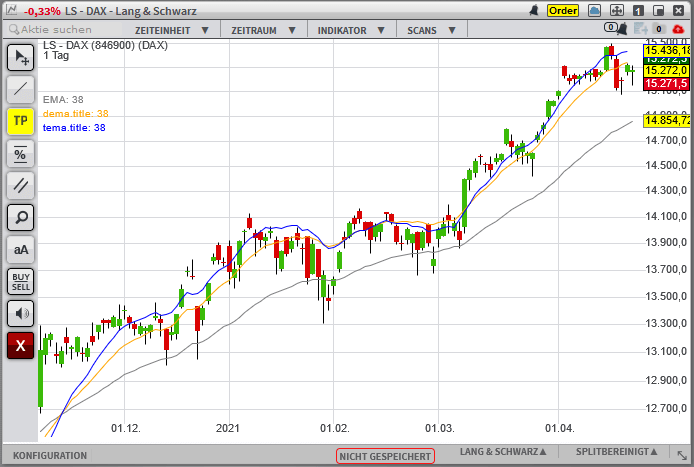
Im Chart sieht man den EMA (grau), den DEMA (orange) und den TEMA (blau). Man erkennt, dass der DEMA und der TEMA wesentlich näher am Chart verlaufen als der EMA.
Weighted Moving Average (WMA)
Der Weighted Moving Average ist eine weitere Abwandlung des Simple Moving Average. Auch hier werden die zur Berechnung herangezogenen Schlusskurse unterschiedlich gewichtet. Im Gegensatz zum Exponential Moving Average nimmt beim Weighted Moving Average die Gewichtung linear ab, wobei die neuesten Werte am höchsten gewichtet werden. Beispielsweise wird im Falle einer 10-Tage-Linie der Schlusskurs des zehnten Tages mit zehn multipliziert, der neunte mit neun, der achte mit acht und so weiter. Die Summe dieser Werte wird anschließend durch die Summe der Multiplikatoren dividiert.
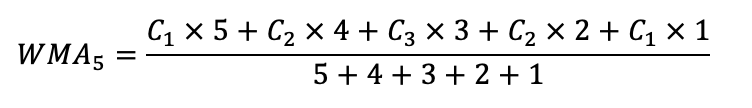
![]()
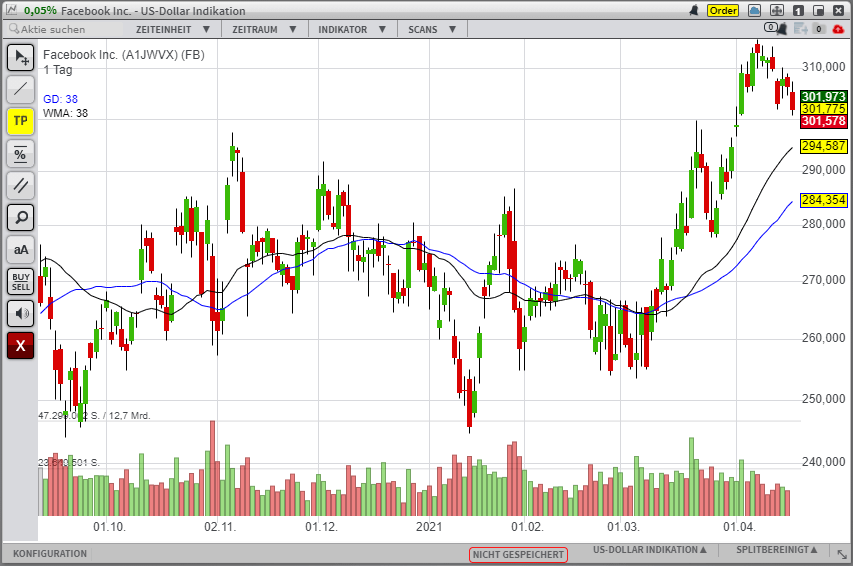
Ähnlich wie der Exponential Moving Average passt sich auch der Weighted Moving Average (schwarz) stärker dem Preisverlauf an.
Hull Moving Average (HMA)
Der Hull Moving Average wurde von Alan Hull entwickelt und ist ein Moving Average, der sehr schnell auf Preisänderungen reagiert. Zur Berechnung benötigt man zuerst den WMA der Periode n/2. Dieser Moving Average wird anschließend mit 2 multipliziert. Zusätzlich benötigt man einen WMA der Periode n. Nun wird noch ein WMA de Periode gebildet. Mit dieser Formel kann dann der HMA berechnet werden:
![]()
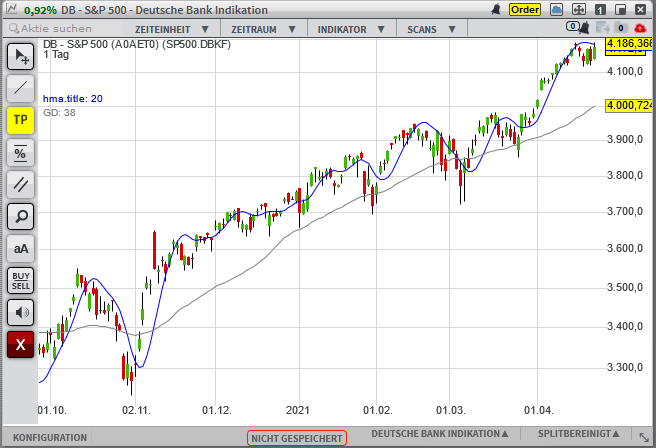
Der HMA (blau) reagiert sehr viel schneller auf Preisänderungen als der SMA (grau).
Triangular Moving Average (TMA)
Der Triangular Moving Average ist ein Moving Average, der zweimal geglättet wird. Er ist somit der mittlere Durchschnitt der mittleren Durchschnitte. Es werden zunächst mehrere Simple Moving Averages berechnet. Anschließend wird der Durchschnitt aller SMA-Werte gebildet:
![]()
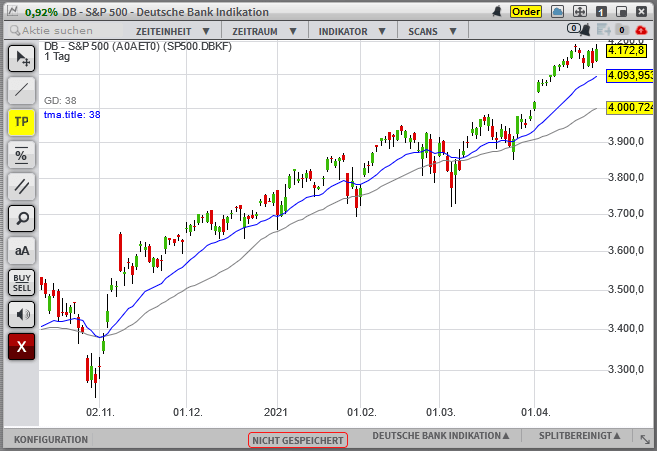
Der TMA (blau) reagiert schneller auf Preisänderungen als der SMA (grau).
Displaced Moving Average (DMA)
Ein Displaced Moving Average funktioniert exakt wie ein gewöhnlicher Moving Average, jedoch mit dem Unterschied, dass dieser zeitlich nach vorne, oder hinten verschoben wurde. Durch dieses Verschieben kann der MA besser an individuelle Werte angepasst werden. Hat man in der Vergangenheit also festgestellt, dass der MA oft Fehlsignale erzeugt, kann ein Verschieben des Indikators dazu führen, dass die Zwischentiefs eines Charts besser getroffen werden und somit die Aussagekraft von Signalen steigt.
Für den DMA gibt es keine eigene Berechnung, da er sich in seiner Funktionsweise nicht von einer MA unterscheidet. Die Berechnung ist somit die Gleiche wie bei der SMA.
Eine Verschiebung des SMA's um 7 Perioden nach vorne, sorgt für exakte Berührungspunkte mit den Zwischentiefs und somit für eine höhere Aussagekraft
Least Square Moving Average (LSMA)
Der Least Square Moving Average (LSMA) berechnet die Regressionsgerade nach der Methode der kleinsten Quadrate (KQ-Methode) für die vorangegangenen Zeiträume und liefert so eine Vorwärtsprojektion für den aktuellen Zeitraum. Das Problem des normalen gleitenden Durchschnitts ist, dass sich dieser weiter in Richtung des Trends bewegt, auch wenn der Trend gestoppt ist. Der LSMA soll Abhilfe schaffen und mithilfe der Regression anzeigen, was passieren könnte, wenn sich der Trend fortsetzt.
Der Indikator basiert auf linearer Regression. Lineare Regression ist eine statistische Methode, um die bestmögliche Gerade zu finden, die man durch eine Streuung legen kann. Gesucht ist also eine Geradengleichung y = m * x + b
Diese wird mithilfe der Methode "Kleinste quadratische Abweichung" (auch KQ-Methode genannt) bestimmt:
![]()
xi sind dabei die jeweiligen Werte auf der x-Achse, yi die jeweiligen Werte auf der y-Achse (Hier: die Schlusskurse). x̄ und y̅ sind die jeweiligen Mittelwerte.
Wenn man die Abstände der Punkte des Streudiagramms zur Regressionslinie aufsummiert, erhält man so den kleinstmöglichen Wert, also die bestmögliche Gerade, um die Streuung abzubilden.
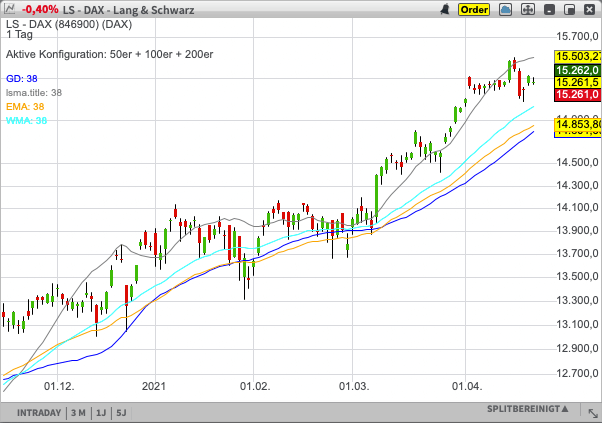
In dem Chart wird der Unterschied zwischen dem SMA (blau), dem EMA (orange), dem WMA (hellblau) und dem LSMA (grau) deutlich. In diesem Fall beträgt die Periodenlänge für jeden Moving Average 38.
Interpretation
Im Folgenden wird bei der Erläuterung nur auf den Simple Moving Average eingegangen, da dieser am häufigsten verwendet wird. Alternativ können aber auch unterschiedliche Weiterentwicklungen des Simple Moving Average gebildet werden. Häufig wird in der Praxis nur ein einziger Moving Average verwendet, um Trendsignale hervorzurufen. Ein Kaufsignal wird dann generiert, wenn der Schlusskurs eines Tages über dem Moving Average liegt. Zu beachten ist dabei, dass ein kurzer Durchschnitt sehr viele Signale generiert, während ein langer Durchschnitt weniger Signale generiert.
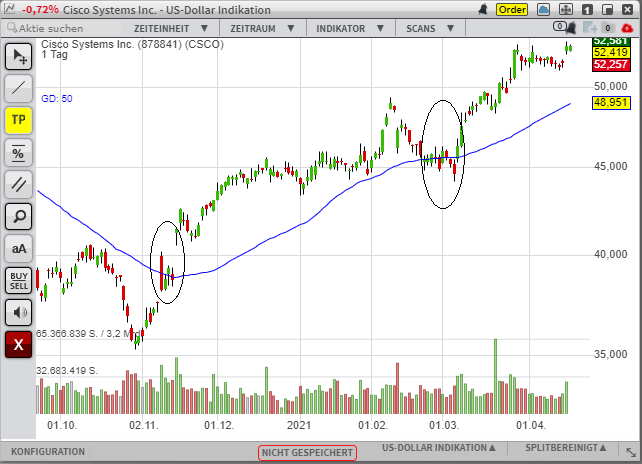
Der Schlusskurs über der 50-Tage-Linie. Das Kaufsignal wird besonders im November dadurch verstärkt, dass der Simple Moving Average stark mit nach oben dreht.
Sehr häufig werden auch zwei Moving Averages benutzt, um Handelssignale zu generieren. Diese Methode wird auch als "Double Crossover Method” bezeichnet. Hierfür wird ein kürzerer und ein längerer Moving Average verwendet. Ein Kaufsignal entsteht dann, wenn der kürzere Durchschnitt den längeren von unten nach oben schneidet. Hierfür wird gerne die 5- und 20-Tage-Linie oder die 10- und 50-Tage-Linie genutzt. Diese Methode generiert die Signale meist erst später als die Benutzung von nur einem Moving Average, ist dafür aber zuverlässiger.
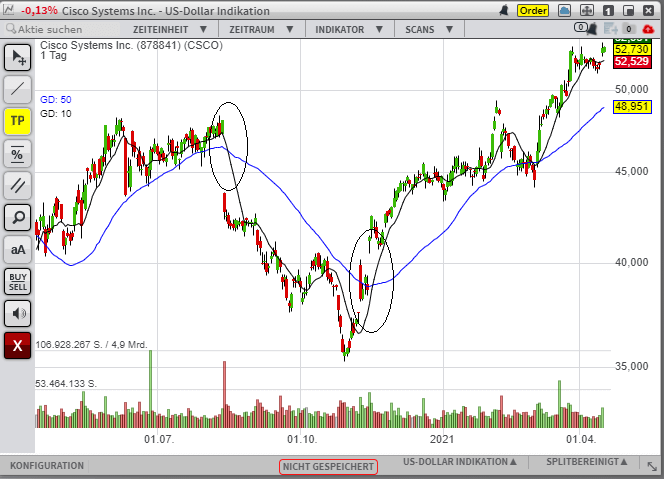
Zuerst wurde aufgrund des großen Gaps ein Verkaufssignal generiert, anschließend schneidet die 10-Tage-Linie die 50-Tage-Linie von unten nach oben und es entsteht ein Kaufsignal.
Auch bei längerfristigen Trendanalysen kann mit einem Moving Average gearbeitet werden. Beispielsweise kann mit der 200-Tage-Linie analysiert werden, ob der langfristige Trend in Takt ist. Die 200-Tage-Linie sollte dabei als Unterstützung dienen.
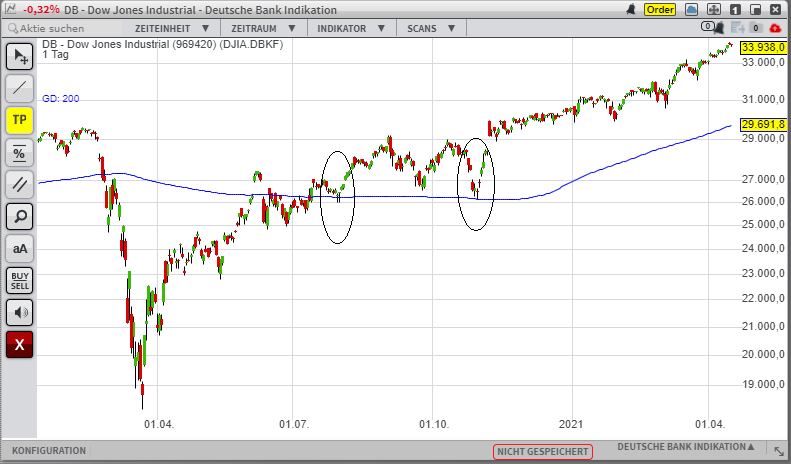
Die 200-Tage-Linie dient als Unterstützung.




